Memoisation is a common technique applied to reduce unnecessary repeated calculations in programming. This technique is frequently brought up as one of the dynamic programming techniques, and in articles, books aiming to help you get your first developer job.
In this article, you'll:
- learn what memoisation is
- take a look at how memoisation can be implemented with a homemade solution
- learn to achieve memoisation using the one-liner
@lru_cachein Python - learn to inspect the cache info of a memoised function
- explore the control knobs of
@lru_cache - learn about the caveats when using
@lru_cache-decorated functions
If you're already familiar with the concept of memoisation, feel free to skip the first section.
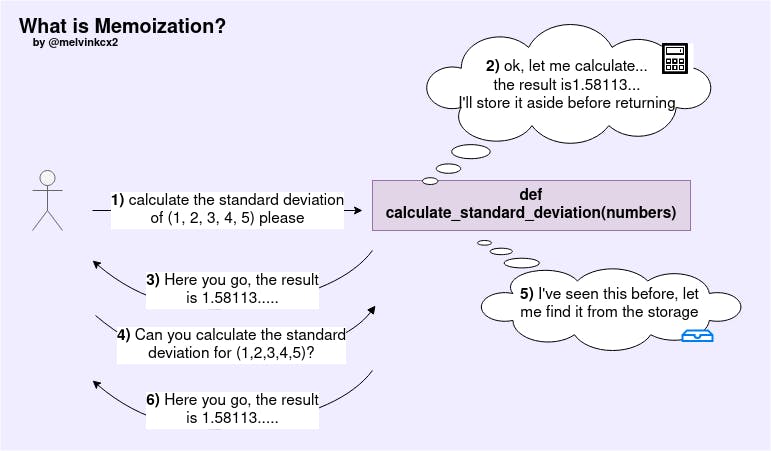
What is Memoisation?
Memoisation is a technique used to ensure the results of a function is stored for the given arguments. Subsequent function invocations with the same arguments should be immediately returned with the previously-stored result.
Implementing Memoisation With A Homemade Solution
There are ways to achieve memoisation. In Python, a decorator is a stark candidate. Let's say we defined a function called calculate_variance() that doesn't possess any abilities to remember any previously calculated results:
from typing import Tuple
import statistics
def calculate_variance(numbers: Tuple[int]):
return statistics.variance(numbers)
To make our calculate_variance() memoise the previously calculated results, there is no need to reimplement the logic to calculate variance. Instead, we would use a @memoise decorator as mentioned.
Eagle-eyed readers may also notice the input argument
numbersis typed withTuple[int], you will see why aTupleinstead of aListis used in the last section.
from typing import Tuple
import statistics
@memoise # This is not implemented yet
def calculate_variance(numbers: Tuple[int]):
return statistics.variance(numbers)
How should we implement the @memoise decorator? I've heard you ask. A simple implementation would be a function that keeps tracks of the input arguments and results in a hashmap and performs calculations only when the results are not found.
from typing import Tuple
def memoise(target_function):
memo = {}
def wrapper(number: Tuple[int]):
hashed_number = hash(number)
if number not in memo:
memo[hashed_number] = target_function(x)
return memo[hashed_number]
return wrapper
The @memoise decorator should work fine with our calculate_variance() function. However, often time, we may come across situations where we need to tailor the memoisation behaviour. For instance, we may want to limit the size of the hashmap, or inspect if the memoised function is working as intended. Fortunately, Python comes with a built-in decorator @lru_cache that gives us the customisability we need.
@lru_cache - The One-Liner To Memoise In Python
@lru_cache is a built-in decorator provided by the functools package that adds memoisation capability to any functions decorated. Strictly speaking, it works not just with functions but any Callable.
Let's rewrite our calculate_variance() function with the @lru_cache decorator.
from functools import lru_cache # Add this line
from typing import Tuple
import statistics
@lru_cache
def calculate_variance(numbers: Tuple[int]):
return statistics.variance(numbers)
With slight changes, we implemented another memoised version of calculate_variance(). Let's invoke and observe our memoised calculate_variance() with the same set of arguments several time.
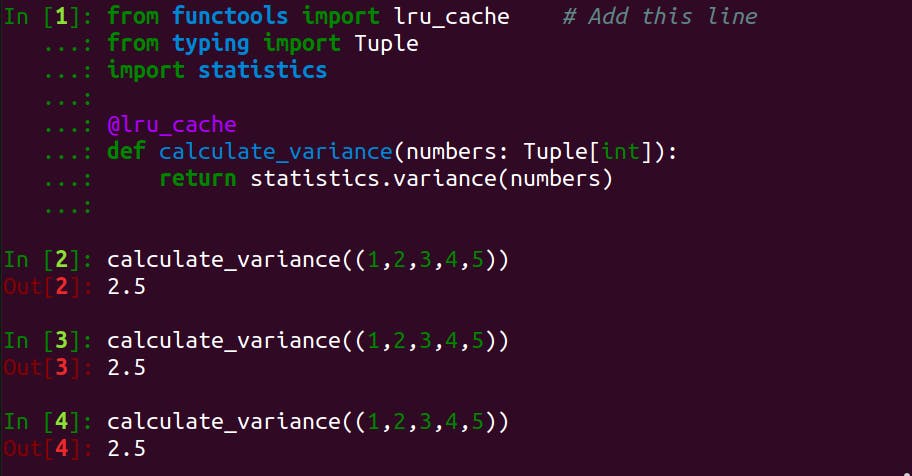
We can clearly see that the function is working correctly. However, how do we know if the values returned are the memoised values?
Inspecting Memoisation Info Using cache_info()
Thanks to @lru_cache, the memoised function now includes a useful method to allow us to peek into the memoisation information (or cache info).
Let's take a look at the screenshot below:
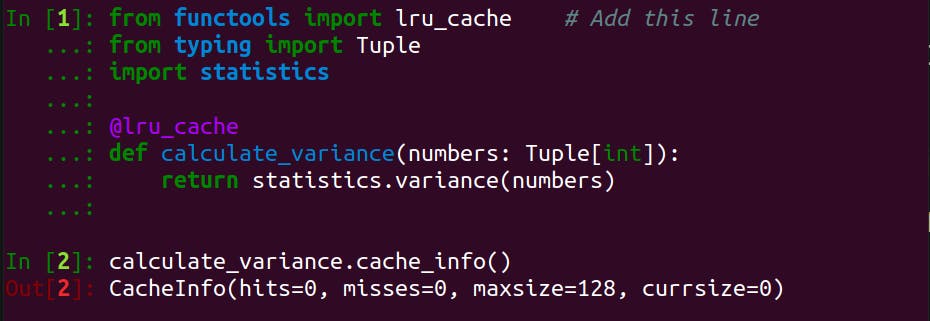
In In[2], calculate_variance.cache_info() is called immediately after the definition of calculate_variance(). From Out[2], we can see a bunch of cache info, including hit, miss, maxsize, and cursize, but what are those?
- cache hit (
hit): number of times when a memoised result is found - cache miss (
miss): the contrary of cache hit, or the number of times when calculations are required - maximum cache size (
maxsize): the maximum number of memoised results stored - current cache size (
cursize): the current number of memoised results stored
Let's try to invoke calculate_variance() with the same argument a few more times and inspect the cache info.
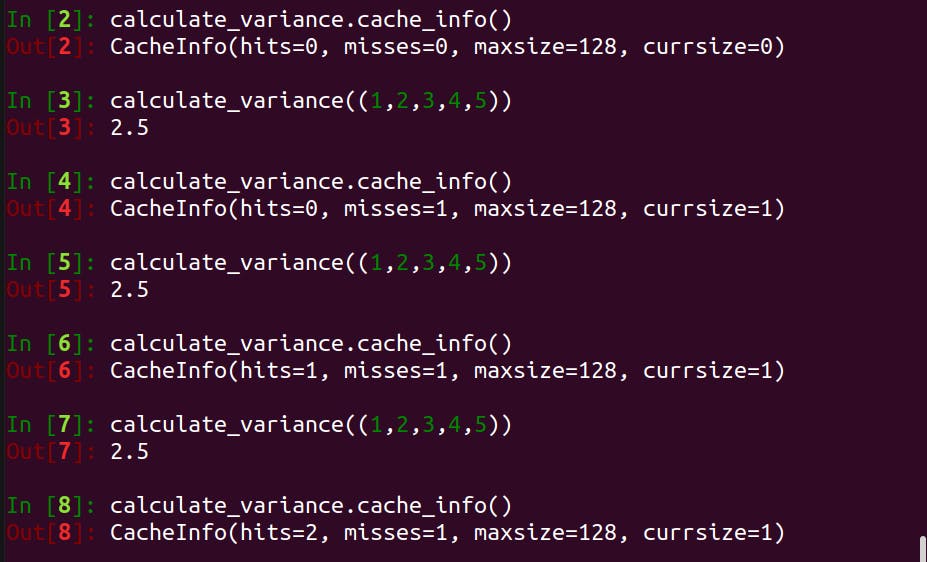
As you can see, the cache hit increases as the function is called with the same argument. ✌️✌️✌️
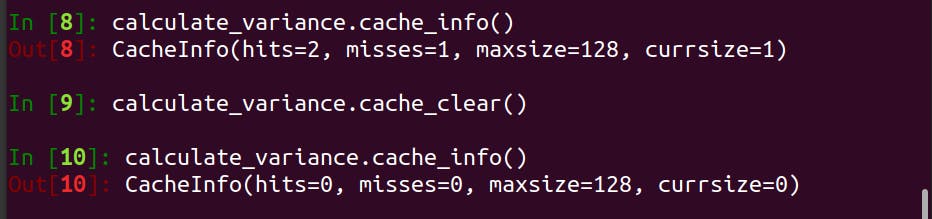
Clearing Memoised Results
While I can't think of a good situation where a cache purge is required, @lru_cache includes a handy method cache_clear() to purge the memoised results.
The Control Knobs Of @lru_cache
typed - Treat Values Of Different Types As Separate Entries
Is the integer 2 the same as 2.0? While 2 == 2.0 is evaluated to True, we recognise they are of different types, int and float. The second control knob of @lru_cache allows us to treat values with different types as separate cache entries. By default, the value of the keyword argument typed is False.
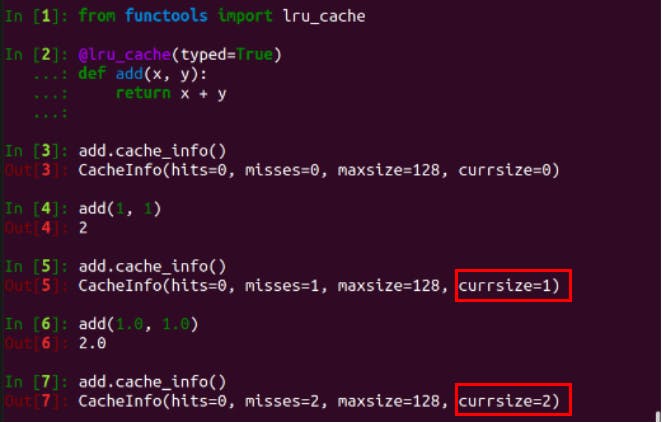
From the screenshot above, we can see the cursize grows when add() is called with the numbers but of different types.
maxsize - The Maximum Size Of The Cache
As mentioned earlier, @lru_cache allows us to tune the maximum size of the cache. To do so, simply pass the keyword argument maxsize into the decorator as shown:
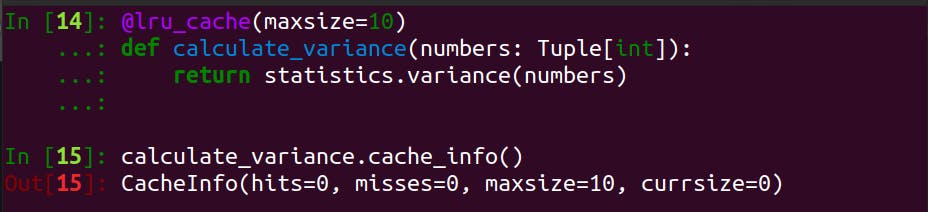
If we want unlimited cache size, all we need is to set maxsize to None.
What Happens When Cache Space Runs Out?
The cache replacement policy of @lru_cache is obviously LRU or Least Recently Used. What does that mean though?
Before we think about when to replace a memoised value, let's think about when a replacement is required. Recapping how memoisation works, we know that after a new calculation is performed, the new result would be stored in the memoised results (or cache) before returning value to the caller.
With the LRU cache replacement policy, when a new result is produced and the cache is full (cursize == maxsize), the least recently used pair will be replaced with the newer pair.
Caveats When Using @lru_cache-Decorated Functions
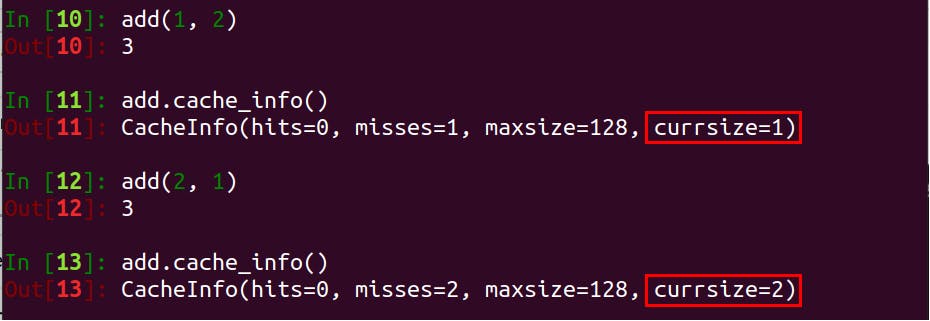
Order of Arguments Matters
@lru_cache treats add(1, 2) and add(2, 1) as two distinct arguments set.
Arguments Must Be Hashable
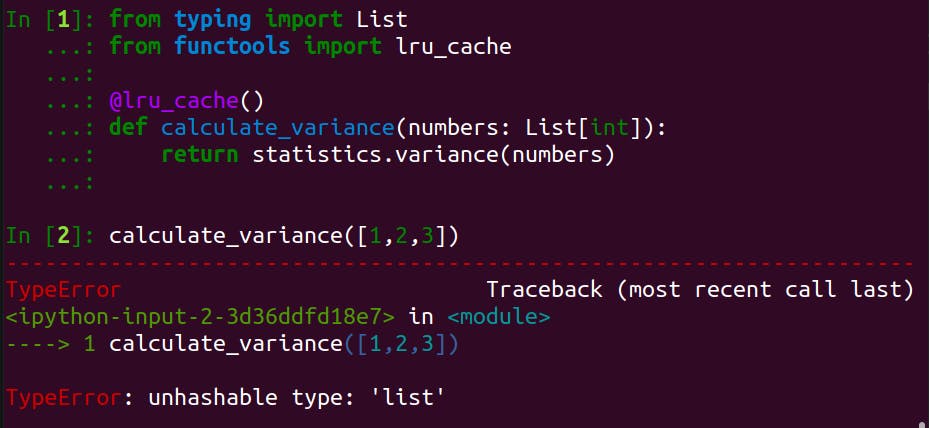
In our example of calculate_variance(), we typed the input argument numbers with Tuple[int].

It is because all input arguments passed to a memoised function must be hashable.
What does hashable mean? According to the official Python glossary, a value is considered hashable if it has a hash value which never changes during its lifetime and can be compared with another value of same type.
Hashability makes an object usable as a dictionary key and a set member, because these data structures use the hash value internally.
How do we know if a value is hashable? A quickiest way is to try to hash the value with the built-in hash() function.
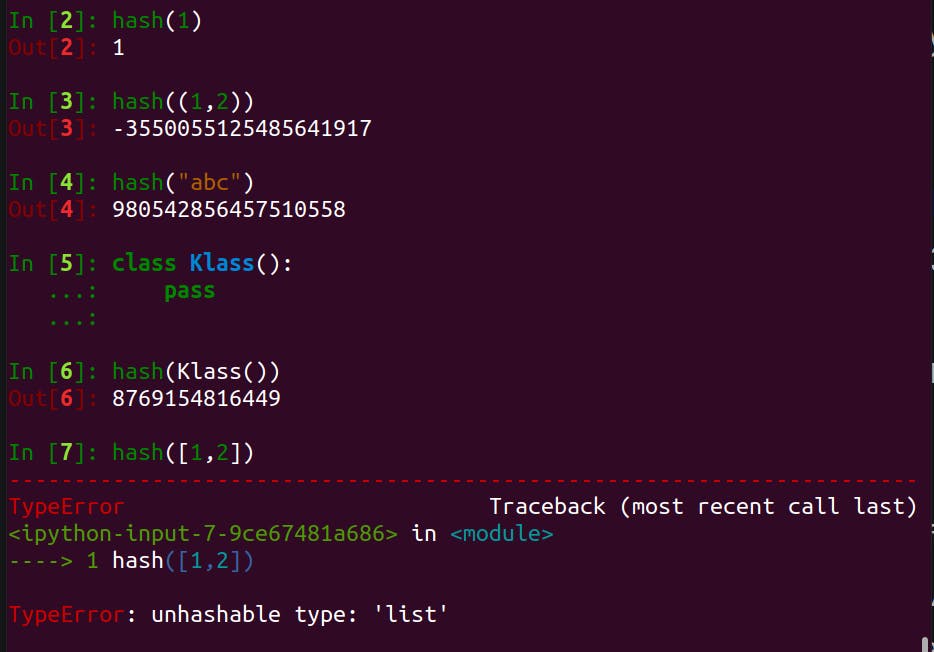
From the screenshot above, we could see that all immutable values are hashable, as well as user-defined class instances. However, Python built-in mutable containers (list, dict, etc) are not.
If we call a memoised (or @lru_cache-decorated) function with a unhashable type, a TypeError will be raised.
Conclusion
By now, you should know:
- what memoisation is
- how the one-liner
@lru_cacheworks in Python - how to inspect the caching info of a memoised function
- the control knobs
typedandmaxsizeof@lru_cache - the caveats when using
@lru_cache-decorated functions
Python functools package provides more than just the @lru_cache. I recommend you to check it out! 🧐
I hope this article helps. Feel free to share it with your mates. I appreciate if you could give this article some claps 👏👏👏.

